MATLAB 을 이용하여 적분을 수행해 보자. MATLAB 을 이용하여 적분을 하는 방법은 크게 두 가지 정도로 구분 할 수 있을 것 같다.
첫 번째로는 수치적인 적분 방법이고 두 번째는 Symbolic math toolbox 를 이용한 수학적인 접근 방법이다.
수치적인 접근 방법이라 하면 사다리꼴 방법 과 같이 함수를 매우 작은 조각으로 나눠서 부분부분의 면적의 합을 구하는 방법이 될 것이다. 물론 이런 적분을 구하는 알고리즘을 짜서 적분을 할 수도 있겠지만 고맙게도 matlab 은 이런 함수를 제공 해 준다.
quad() 함수를 이용하면 수치 적분이 가능하다. 본 함수는 수치 적분이므로 부정적분을 해 주지는 못한다. 따라서 다음 수식과 같이 구간이 정해진 식에 대해서만 적분 할 수 있다.

위 수식에 대한 적분은 다음과 같다.
F = @(x) x.^2+2.*x+1
F =
@(x)x.^2+2.*x+1
quad(F,0,3)
ans =
21
간단하게 해가 나오는 것을 확인 할 수 있다.
하지만 이런 수치적분은 위에서 밝힌 대로 부정적분이 불가능 하다. 부정적분을 할 때는 symbolic math toolbox 를 이용해야 한다. Symbolic math toolbox 는 Mathematica 나 Maple 과 같이 기호로서 계산을 해주는 툴로서 복잡한 수학 계산시 굉장히 편리하게 이용할 수 있다.
다음과 같은 수식에 대해 간단하게 부정적분 그리고 임의의 구간에 대한 적분을 수행 해보자.

부정적분은 굉장히 간단하다.
symbol 로 사용한 변수인 x 를 symbolic 으로 설정해준다.
syms x
int(x^2+2*x+1)
그리고 int() 함수 내에 적분할 수식을 써 준다. int() 함수는 integral 의 약자이다. 위 코드의 실행 결과는 다음과 같은 부정적분 결과가 나온다.
ans =
(x*(x^2 + 3*x + 3))/3
그럼 임의의 구간 a~b 구간에 대해서도 적분을 해 보자. a, b 도 symbolic 으로 설정을 해 준 후에 int() 함수에서 적분 구간을 a, b 라고 명시 해 준다.
syms x a b
int(x^2+2*x+1,a,b)
ans =
b*(b*(b/3 + 1) + 1) - a*(a*(a/3 + 1) + 1)
다음과 같이 간단하게 a, b 라는 적분구간에 대해 적분이 실행 되는 것을 확인 할 수 있다.
'programming language > MATLAB' 카테고리의 다른 글
| MATLAB subplot() (0) | 2011.03.16 |
|---|---|
| MATLAB 입력 신호의 delay 확인 xcorr(), finddelay() (0) | 2011.03.14 |
| MATLAB 벡터화 기법 (0) | 2011.03.14 |
| MATLAB 적분 추가 내용 trapz() (0) | 2011.03.14 |
| MATLAB 함수의 해를 구해 보자~ fzero(), roots(), poly() (2) | 2011.03.13 |
| MATLAB ezplot() 함수로 그래프를 쉽게 그리자 (2) | 2011.03.13 |
| MATLAB 다항식의 계수 추정 polyfit(), polyval() (0) | 2011.03.12 |
| MATLAB 소스 코드 protection, pcode (1) | 2011.03.11 |

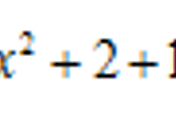


댓글